What Are Perfect Squares and Perfect Cubes?

Q: What Are Perfect Squares and Perfect Cubes?

A: Discovering Patterns: Perfect Squares, Perfect Cubes, and the Beauty of Mathematics

Have you ever noticed how numbers can have a hidden rhythm and harmony? Understanding these patterns can make mathematics not just easier, but genuinely fascinating. Two fundamental concepts that showcase this beauty are perfect squares and perfect cubes. Let’s explore them in a simple and intuitive way.

There is a certain uniformity in these patterns, and it is this very uniformity that creates beauty. Mathematics, in many ways, is a lens through which we can perceive order and elegance in the world. Learning about perfect squares and perfect cubes is a small but significant step toward recognising the aesthetic patterns hidden in numbers.

And it’s not just numbers. The beauty we see around us—in nature, architecture, and art—is often a reflection of the same mathematical uniformity. From the petals of a flower to the proportions of a building, the world follows patterns that mirror the harmony found in mathematics.

1. Perfect Squares

A perfect square is a number that can be expressed as the product of an integer with itself. In other words, if you multiply a number by itself, the result is a perfect square.

Formula:

\[
\text{Perfect Square} = n \times n = n^2
\]

Here, n is any integer.

Examples:

• \[1 \times 1 = 1\] → 1 is a perfect square
• \[2 \times 2 = 4\] → 4 is a perfect square
• \[3 \times 3 = 9\] → 9 is a perfect square
• \[10 \times 10 = 100\] → 100 is a perfect square

Tip to Remember:
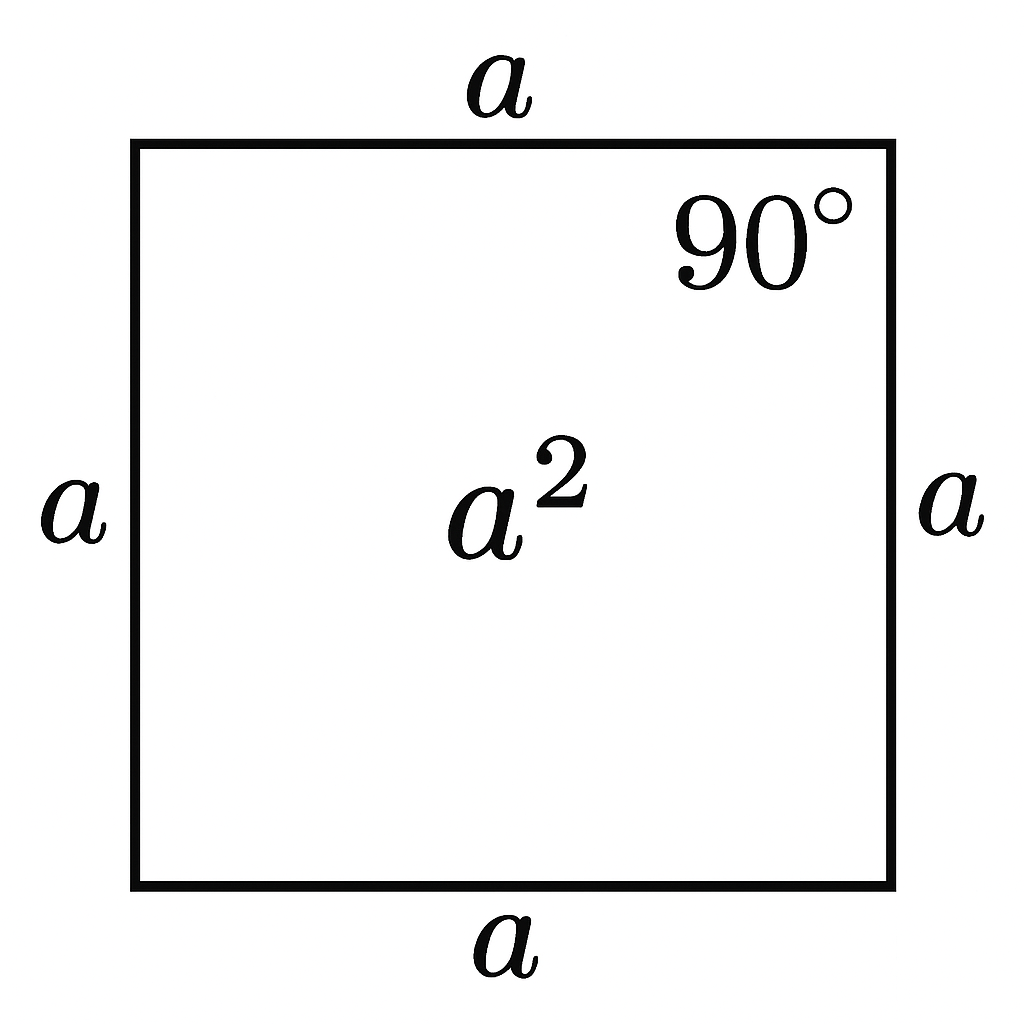
Think of a perfect square as forming a square shape. For example, if you have 9 dots, you can arrange them in a perfect 3×3 square. That’s why it’s called a perfect square.

Shown in the figure is a perfect square, and each side has a length of a.

2. Perfect Cubes

A perfect cube is a number that can be expressed as the product of an integer multiplied by itself three times. Essentially, if a number is used as the length, breadth, and height of a cube, the result is a perfect cube.

Formula:

\[
\text{Perfect Cube} = n \times n \times n = n^3
\]

Here, n is any integer.

Examples:

• \[1 \times 1 \times 1 = 1\] → 1 is a perfect cube
• \[2 \times 2 \times 2 = 8\] → 8 is a perfect cube
• \[3 \times 3 \times 3 = 27\] → 27 is a perfect cube
• \[4 \times 4 \times 4 = 64\] → 64 is a perfect cube

Quick Comparison Table

Concept	Formula	Example Numbers	Shape to Imagine
Perfect Square	\[n^2\]	1, 4, 9, 16, 25	Square (2D)
Perfect Cube	\[n^3\]	1, 8, 27, 64, 125	Cube (3D)

Why Learning Perfect Squares and Cubes is Important

• Quick calculations: They help in mental math and solving problems faster.
• Algebra: They are foundational in learning quadratic and cubic equations.
• Geometry: Perfect squares and cubes help in understanding area and volume.
• Number patterns: Recognising these numbers improves logical thinking.

First 50 Perfect Squares and Cubes

n	Perfect Square (n²)	Perfect Cube (n³)
1	1	1
2	4	8
3	9	27
4	16	64
5	25	125
6	36	216
7	49	343
8	64	512
9	81	729
10	100	1000
11	121	1331
12	144	1728
13	169	2197
14	196	2744
15	225	3375
16	256	4096
17	289	4913
18	324	5832
19	361	6859
20	400	8000
21	441	9261
22	484	10648
23	529	12167
24	576	13824
25	625	15625
26	676	17576
27	729	19683
28	784	21952
29	841	24389
30	900	27000
31	961	29791
32	1024	32768
33	1089	35937
34	1156	39304
35	1225	42875
36	1296	46656
37	1369	50653
38	1444	54872
39	1521	59319
40	1600	64000
41	1681	68921
42	1764	74088
43	1849	79507
44	1936	85184
45	2025	91125
46	2116	97336
47	2209	103823
48	2304	110592
49	2401	117649
50	2500	125000

📂 Download PDF: First 50 Perfect Squares and Cubes

Conclusion:

Perfect squares and perfect cubes are simple concepts once you visualise them. Squares relate to multiplying a number by itself, forming a 2D square. Cubes relate to multiplying a number three times, forming a 3D cube. With practice, you’ll start spotting them instantly in mathematics.